Die Hobbits Bilbo und Frodo Beutlin feiern gemeinsam Geburtstag. Als besondere Überraschung hat Kerzenziehermeister Rudigar Wachsdreher Geburtstagskerzen unterschiedlichster Form kreiert.
Alle haben zu Beginn die gleiche Höhe und das gleiche Volumen. Es kann davon ausgegangen werden, dass jede Kerze pro Minute die gleiche Menge an Wachs verbrennt.
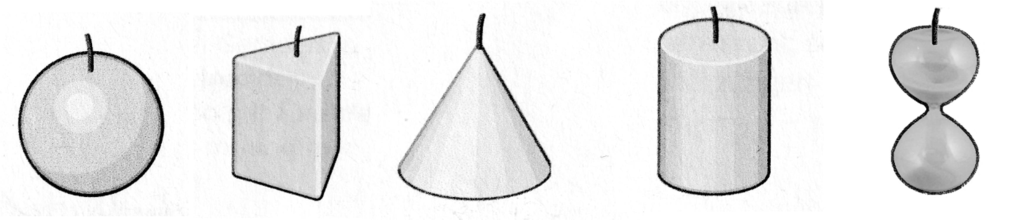
a) Begründen Sie kurz, welche der vier zuerst abgebildeten Kerzen das Abbrennverhalten des eingezeichneten Graphen (Höhe h in cm in Abhängigkeit von der Brenndauer t in min) zeigt.
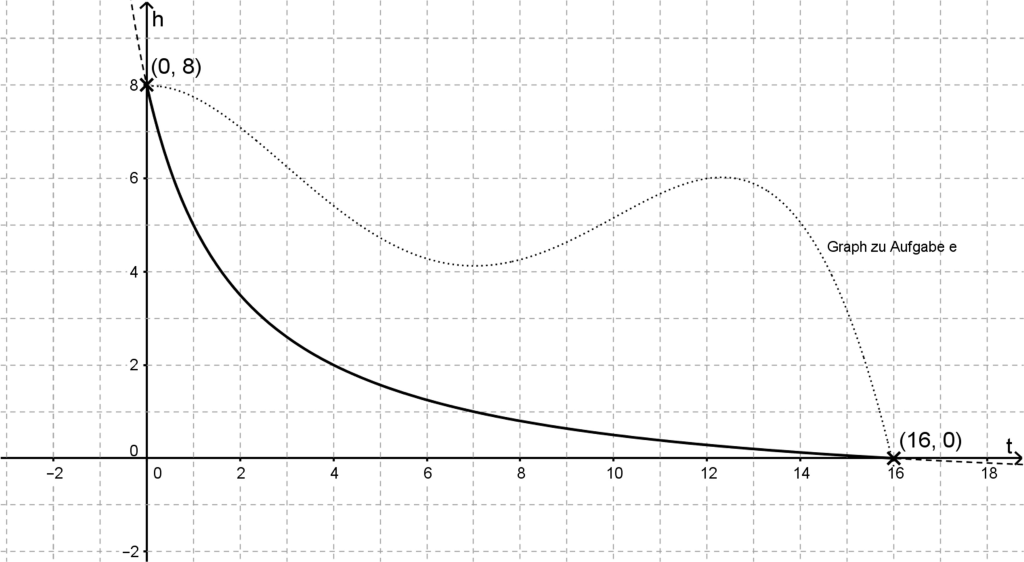
b) Bestimmen Sie die mittlere Abbrenngeschwindigkeit v dieser Kerze. Ermitteln Sie außerdem, nach wie vielen Minuten die momentane Abbrenngeschwindigkeit etwa der mittleren Abbrenngeschwindigkeit entspricht.
c) Skizzieren Sie in das Koordinatensystem den Graphen s(t) einer sanduhrförmigen Kerze.
d) Der oben abgebildete Graph gehört zu genau einer der folgenden Funktionen. Finden Sie für die drei anderen je einen Grund, der sie ausschließt. Jede Begründung (z.B. Nullstellen, abweichender Funktionswert, …) darf nur einmal verwendet werden!
\[h_1(x)=x-16+\frac{1}{x+2}\] \[h_2(x)=\frac{x-16}{x+2}\] \[h_3(x)=-\frac{x-16}{x+2}\] \[h_4(x)=-\frac{1}{2}x+8\]e) Peregrin „Pippin“ Tuk, der ausgiebig mitgefeiert hat, behauptet am nächsten Morgen, er habe eine Kerze so abbrennen sehen, wie es der gepunktete Graph anzeigt. Beurteilen Sie seine Aussage kurz.

